EN 2011 Física - Questões
Abrir Opções Avançadas
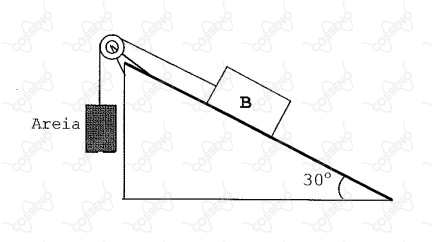
Na figura abaixo, temos o bloco $B$ de massa igual a $4,0\ kg$ e um
recipiente (massa desprezível) cheio de areia, interligados por um fio
(inextensível e de massa desprezível) que passa por uma polia ideal. Os
coeficientes de atrito estático e cinético entre o bloco $B$ e a reta de
maior declive do plano inclinado valem, respectivamente, $0,050 \sqrt{3}$ e
$0,040\sqrt{3}$. O recipiente possui um pequeno orifício no fundo, por onde a
areia pode sair. No instante $t=0$,a massa da areia no recipiente é de
$1,7 kg$. A partir do instante $t = 0$, com a areia saindo do orifício, o
módulo da maior aceleração (em $m/^2$) adquirida pelo bloco $B$ é
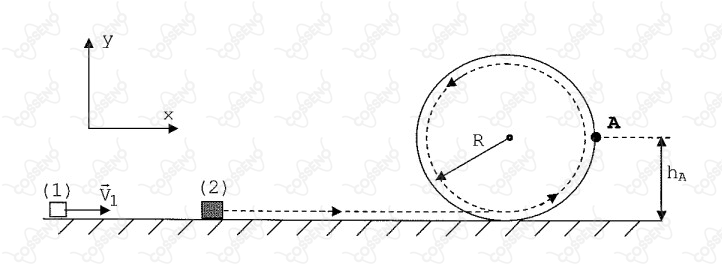
Uma pista é composta por um trecho retilíneo longo horizontal
seguido do trecho circular vertical de raio $R$ (conforme a figura
abaixo). O carrinho (1) (partícula), de massa $m_1 = 1,0\ kg$ e velocidade
$\vec{V_1} =5,0.\widehat{i}\ (m/s)$, colide com o carrinho (2) (partícula), de massa $m_2= 2,0\ kg,$
em repouso no trecho retilíneo. Despreze os atritos. O coeficiente de
restituição do choque vale $0,80$. Após a colisão, o carrinho (2) sobe o
trecho circular vertical e, num certo instante, passa pela primeira vez
na posição $ A$, de altura $h_A=R$, com velocidade tal que o módulo da força
normal da pista sobre o carrinho é igual ao módulo do seu peso.
Nesse instante, o módulo da velocidade (em $m/s$) do carrinho (2) em
relação ao carrinho (1) é
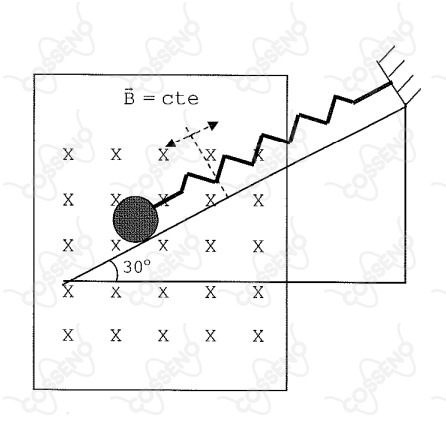
Uma pequena esfera carregada, de massa $m=0,400\ kg$ e carga elétrica
$q=7,50\times10^{-1}\ C$, está presa à mola ideal de constante elástica $K=40,0\ N/m$. O sistema esfera -mola oscila em M.H.S, com amplitude $A=10,0\ cm$, sobre
uma rampa formando uma ângulo de $30^°$ com a horizontal. A esfera move-se
numa região onde existe um campo magnético uniforme de módulo igual a
$2,00$ teslas, perpendicular ao plano do movimento (conforme a figura
abaixo). Despreze os atritos e a magnetização da mola. No instante em
que a mola estiver esticada $10,0\ cm$ em relação ao seu tamanho natural,
se afastando da posição de equilíbrio do sistema esfera-mola, o módulo
da força normal (em newtons) exercida pelo plano inclinado (rampa)
sobre a esfera é
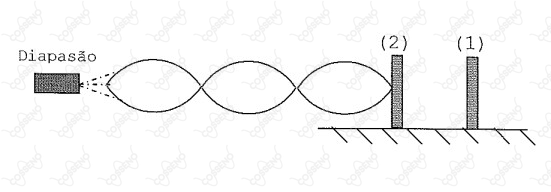
Uma corda isolante de massa $m$ e comprimento $L$ está esticada, com as
extremidades presas a um diapasão e à placa (2) de um capacitor plano
de placas paralelas, a vácuo. A área de cada placa do capacitor é $A$ e,
inicialmente, ele está carregado com carga elétrica de valor absoluto
igual a $400\ uC$. A placa (1) do capacitor está fixa e a placa (2) pode se
mover somente na direção horizontal, entre duas guias não representadas
na figura. Despreze os atritos. A frequência de vibração do diapasão é
igual a $300 \ Hz $ e a corda está oscilando no $3^o$ harmônico (conforme a
figura abaixo). Para que a corda oscile no $2^o$ harmônico, o valor
absoluto da nova carga elétrica (em $pC$) que o capacitor deve possuir é
No circuito elétrico abaixo, a chave $ K$ está inicialmente ligada ao terminal (1) e o reostato $R$, é ajustado em $0{,}50\ \Omega$, para que a corrente elétrica indicada no amperímetro seja de $10\text{ A}$. Tal valor de corrente é igual à metade da corrente de curto-circuito do gerador de f.e.m $\varepsilon_1$ e resistência interna $r_1$. Posteriormente, a chave é ligada ao terminal (2) e espera-se pela carga total dos capacitores. Verifica-se, então, que o capacitor C; possui carga elétrica $Q_1=20\ \mu\text{C}$. O valor absoluto da f.e.m $\varepsilon_2$ (em volt) do segundo gerador é:
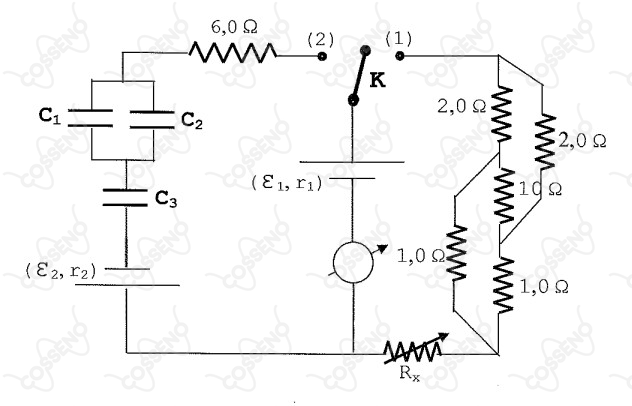
$C_2=4{,}0\ \mu\text{F}$
$C_3=5{,}0\ \mu\text{F}$
Carregando...