CN 2018 - Questões

Sejam os conjuntos $A=\left\{9, \; 27, \; 45, \; ... \; , \; 423, \; 441\right\}$, $B=\left\{18, \; 36, \; 54, \; ... \; , \; 432, \; 450\right\}$, $C=\left\{3 \; 9, \; 15, \; ... \; , \; 141, \; 147\right\}$ e $D=\left\{6, \; 12, \; 18, \; ... \; , \; 144, \; 150\right\}$. Define-se $P_{K}$ como sendo o produto de todos os elementos do conjunto $K$. Nas condições apresentadas, é correto afirmar que a expressão $\dfrac{P_{A} \cdot P_{B} }{P_{C} \cdot P_{D} } \cdot 243^{-10}$ é igual a

Seja $x$ real tal que $\dfrac{3}{x+1} +\dfrac{4}{1-x} =\dfrac{1}{x}$. Sendo assim, o valor de $\left(\dfrac{1}{x^{2} } -\dfrac{7}{x} \right)$ é igual a

Analise a figura a seguir.

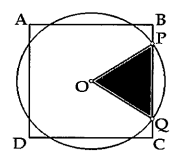
Pelo centro $O$ do quadrado de lado $\sqrt{6}\ \text{cm}$ acima, traçou-se a circunferência que corta o lado $BC$ nos pontos $P$ e $Q$. O triângulo $OPQ$ tem área $\dfrac{\sqrt{3}}{2}\ \text{cm}^{2}$. Sendo assim, é correto afirmar que o raio dessa circunferência, em $\text{cm}$, é igual a

Um triângulo isósceles $ABC$ tem base $BC=16{ \; }$cm e lados congruentes $AB=AC=17{ \; }$cm. O raio do círculo inscrito ao triângulo $ABC$ em $cm$ é igual a:

Sabendo que $5^{k} =561+2^{2p}$ e $5^{\frac{k}{2} } =17+2^{p}$, o valor de $\dfrac{p^{k} -k^{p} }{p^{k} +k^{p} }$ é igual a