AFA 2011 Física - Questões

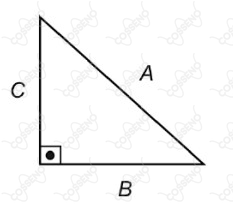
Um turista, passeando de bugre pelas areias de uma praia em Natal — RN, percorre uma trajetória triangular, que pode ser dividida em três trechos, conforme a figura abaixo.

Os trechos B e C possuem o mesmo comprimento, mas as velocidades médias desenvolvidas nos trechos $A, B$ e $C$ foram, respectivamente, $v$, $2v$ e $v$. A velocidade escalar média desenvolvida pelo turista para percorrer toda a trajetória triangular vale

Dois automóveis A e B encontram-se estacionados RASCUNHO paralelamente ao marco zero de uma estrada. Em um dado instante, o automóvel A parte, movimentando-se com velocidade escalar constante $v_A = \pu{80 km/h}$. Depois de certo intervalo de tempo, $\Delta t$, o automóvel $B$ parte no encalço de $A$ com velocidade escalar constante $v_B = \pu{100 km/h}$. Após $\pu{2 h}$ de viagem, o motorista de $A$ verifica que $B$ se encontra $\pu{10 km}$ atrás e conclui que o intervalo $\Delta t$, em que o motorista $B$ ainda permaneceu estacionado, em horas, é igual a

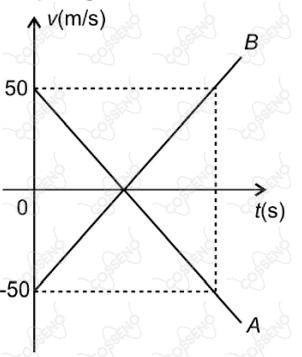
Duas partículas, $A$ e $B$, que executam movimentos retilíneos uniformemente variados, se encontram em $t = O$ na mesma posição. Suas velocidades, a partir desse instante, são representadas pelo gráfico abaixo.

As acelerações experimentadas por $A$ e $B$ têm o mesmo módulo de $\pu{0,2 m/s^2}$. Com base nesses dados, é correto afirmar que essas partículas se encontrarão novamente no instante

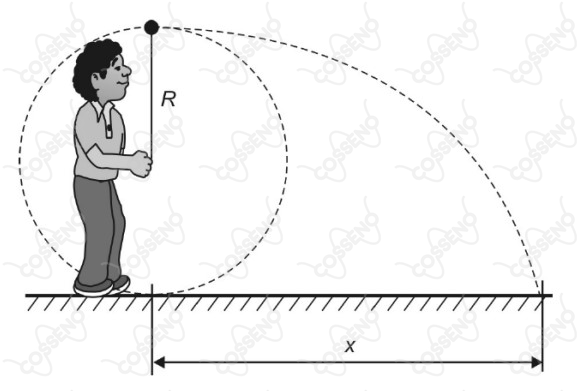
Um garoto, que se encontra em repouso, faz girar, com velocidade constante, uma pedra de massa $m$ presa a um fio ideal. Descrevendo uma trajetória circular de raio $R$ num plano vertical, essa pedra dá diversas voltas, até que, em um dado instante, o fio arrebenta e ela é lançada horizontalmente, conforme ilustra a figura a seguir.

Sujeita apenas à aceleração da gravidade $g$, a pedra passou, então, a descrever uma trajetória parabólica, percorrendo uma distância horizontal $x$ equivalente a $4R$. A tração experimentada pelo fio toda vez que a pedra passava pelo ponto onde ele se rompeu era igual a

Considere que dois vetores $\vec{A}$ e $\vec{B}$ fazem entre si um ângulo de $60º$, quando têm suas origens sobre um ponto em comum. Além disso, considere também, que o módulo de $\vec{B}$ é duas vezes maior que o de $\vec{A}$ , OU Seja, $B = 2A$. Sendo o vetor soma $\vec{S}=\vec{A}+\vec{B}$ e o vetor diferença $\vec{D}=\vec{A}-\vec{B}$, a razão entre os módulos $\frac{S}{D}$ vale