AFA 2009 Física - Questões

O diagrama abaixo representa as posições de dois corpos $A$ e $B$ em função do tempo.

Por este diagrama, afirma-se que o corpo $A$ iniciou o seu movimento, em relação ao corpo $B$, depois de

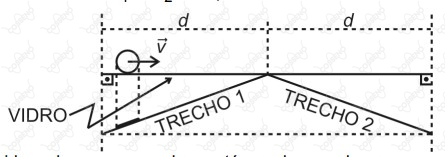
Uma bola rola com velocidade $\vec{v}$ , constante, sobre uma superfície de vidro plana e horizontal, descrevendo uma trajetória retilínea. Enquanto a bola se desloca, a sua sombra percorre os planos representados pelos trechos $1$ e $2$ da figura abaixo, com velocidades escalares médias $v_1$ e $v_2$ , respectivamente.

Considerando que a sombra está sendo gerada por uma projeção ortogonal à superfície de vidro, pode-se afirmar que o seu movimento é

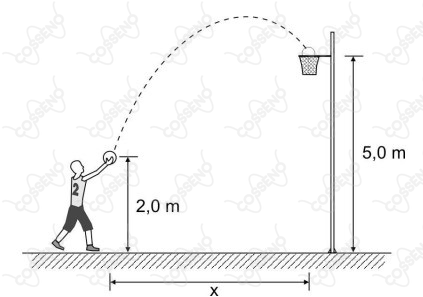
Uma bola de basquete descreve a trajetória mostrada na figura após ser arremessada por um jovem atleta que tenta bater um recorde de arremesso.

A bola é lançada com uma velocidade de $\pu{10 m/s}$ e, ao cair na cesta, sua componente horizontal vale $\pu{6,0 m/s}$. Despreze a resistência do ar e considere $\pu{g = 10 m/s^2}$ . Pode-se afirmar que a distância horizontal ($x$) percorrida pela bola desde o lançamento até cair na cesta, em metros, vale

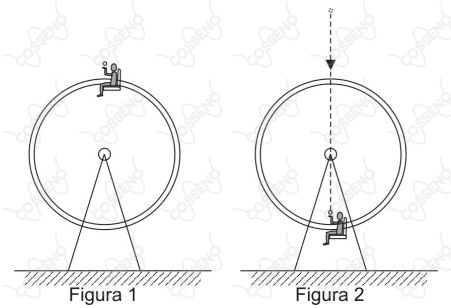
Uma pessoa, brincando em uma roda-gigante, ao passar pelo ponto mais alto, arremessa uma pequena bola (Figura 1), de forma que esta descreve, em relação ao solo, a trajetória de um lançamento vertical para cima.

A velocidade de lançamento da bola na direção vertical tem o mesmo módulo da velocidade escalar ($v$) da roda-gigante, que executa um movimento circular uniforme. Despreze a resistência do ar, considere a aceleração da gravidade igual a $g$ e $\pi = 3$. Se a pessoa consegue pegar a bola no ponto mais próximo do solo (Figura 2), o período de rotação da roda-gigante pode ser igual a

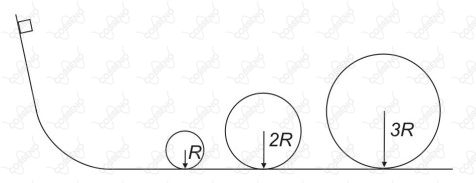
Uma partícula é abandonada de uma determinada altura e percorre o trilho esquematizado na figura abaixo, sem perder contato com ele.

Considere que não há atrito entre a partícula e o trilho, que a resistência do ar seja desprezível e que a aceleração da gravidade seja $g$. Nessas condições, a menor velocidade possível da partícula ao terminar de executar o terceiro looping é