AFA 2008 - Questões

Classifique em (V) verdadeira ou (F) falsa cada afirmativa abaixo sobre o ponto $P(x, y)$ no plano cartesiano.

( ) Se o ponto $P$ pertence simultaneamente às bissetrizes dos quadrantes ímpares e dos quadrantes pares, então o ponto simétrico de $P$ em relação à reta $y = k (k ∈ \mathbb{R}^*)$ tem a soma das coordenadas igual a $2k$

( ) Sendo $\{x, y\} \subset \mathbb{Z}$, então existem apenas dois pontos $P(x, y)$ que atendem às condições $\begin{cases} x< 0 \\ y^2 - 3y \leqslant x\end{cases}$

( ) Os pontos $P(x, y)$ tais que a sua distância ao eixo das abscissas é igual à metade da distância de $P$ ao ponto $Q(0, 6)$ formam uma hipérbole de excentricidade igual a 2

Sobre as afirmativas tem-se

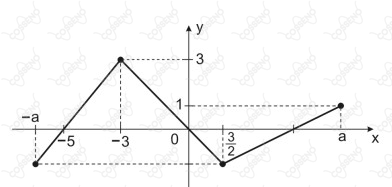
Na figura abaixo, está representado o gráfico da função real $f: [–a, a] \rightarrow \mathbb{R}$, onde $f(0) = 0$

Analise as alternativas abaixo e marque a INCORRETA.

Considere no Plano de Argand-Gauss os números complexos $\mathrm {z_1 = \ –x – 2i}$, $\mathrm{z_2 = \ –2i}$, $\mathrm{z_3 = \ –2 + 3i}$ e $\mathrm{z_4 = x + yi}$, onde $\mathbf x$ e $\mathbf y$ são números reais quaisquer e $\mathrm{i^2 = \ –1}$

Sobre o conjunto desses números complexos que atendem simultaneamente às condições

I) $\mathrm{Re}\,(\mathrm{\overline{z}_{1}\cdot\overline{z}_{2}})\ \leqslant\ \mathrm{lm}\,(\mathrm{\overline{z}_{1}\cdot\overline{z}_{2}})$

II) $| \mathrm{z_3 + z_4}| \leqslant 2$

é correto afirmar que

As funções $f: \mathbb{R} \rightarrow \mathbb{R}$ do 1º grau e $g: \mathbb{R} → [b, +\infty[$ do 2º grau estão representadas no gráfico abaixo.

Com base nas informações acima, é correto afirmar que

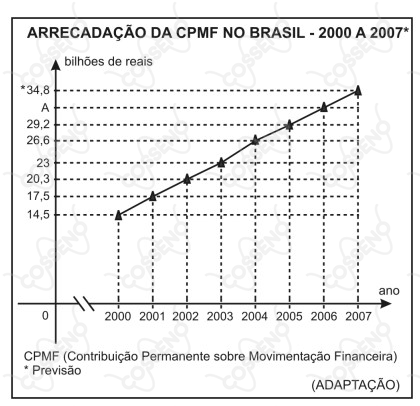
“A arrecadação da CPMF, devido à ampliação de sua abrangência, e ao aumento da alíquota, cresceu mais de 140% nos últimos anos (em bilhões de reais por ano)”

Revista veja – 14/03/2007

Supondo que o crescimento da arrecadação representado no gráfico acima é linear do ano de 2005 ao ano de 2007 e que y% representa o aumento da arrecadação do ano de 2005 ao ano de 2006, é correto afirmar que y é um número do intervalo